La recente pandemia di Covid-19 ha riportato alla ribalta l’importanza della corretta lettura dei dati statistici e la loro interpretazione scientifica, che sono anche alla base della odierna Data Science.
Allo stesso modo, ha reso evidente quanto sia purtroppo largamente diffusa, non solo nell’ambito dei media, ma sorprendentemente
anche in ambiti scientifici come quello medico-sanitario, l’ignoranza dei (o la confusione sui) concetti di base della statistica, in modo particolare di calcolo delle probabilità.
Non dovrebbe quindi meravigliarci la riproposizione di “ragionamenti” fallaci basati sulla confusione tra probabilità condizionali differenti ritornata in auge di recente, a seguito dell’approvazione del testo base sulla cannabis adottato in commissione Giustizia alla Camera, che ha indotto esponenti politici (anche nel recente passato) a rilasciare affermazioni quantomeno discutibili sull’asserito nesso di stringente causalità esistente tra consumo di cannabis e dipendenza da droghe “pesanti”…
Tuttavia, l’incapacità di ragionare correttamente in termini probabilistici induce a decisioni errate non supportate dai dati, che possono avere implicazioni negative in vari settori della vita sociale (a cominciare dalla
corretta valutazione delle prove a carico degli imputati di comportamenti penalmente rilevanti), che contraddicono il saggio ammonimento di Einaudi citato in precedenza.
Ragionare di probabilità in maniera intuitiva
Occorre dire, a parziale comprensione (ma non giustificazione) della difficoltà di ragionare correttamente in termini probabilistici, che i concetti sottostanti al ragionamento statistico sono spesso controintuitivi.
Per rendere appetibile e comprensibile anche ai più ostinati i concetti relativi alle probabilità condizionali, è possibile fare alcuni esempi intuitivi, introducendo una simbologia semplificata come quella mostrata di seguito.
Introduciamo preliminarmente uno scenario di esempio che contribuisca a chiarire le idee.
Immaginiamo di trovarci di fronte ad un individuo sconosciuto, di sesso maschile (particolare importante, come vedremo tra breve) del quale non abbiamo alcuna ulteriore informazione, e con il quale ci apprestiamo ad instaurare una conversazione.
Mettiamo il caso che dalla conversazione veniamo a conoscenza di alcune informazioni che riguardano il soggetto in questione, come ad es. il fatto che egli è uso frequentare assiduamente la parrocchia del nostro stesso quartiere.
Già queste succinte informazioni ci consentono di trarre alcune conclusioni di natura probabilistiche (dette inferenze in gergo tecnico):
possiamo infatti concludere con un certo grado di affidabilità probabilistica (sulla base del nostro bagaglio di conoscenze pregresse) che il soggetto in questione sia di fede cattolica e praticante (a meno che non si voglia prendere in considerazione la possibilità che il soggetto in questione vada in chiesa in alternativa al cinema, possibilità ritenuta inverosimile sempre sulla base delle nostre conoscenze pregresse…)
In termini simbolici, possiamo esprimere l’inferenza probabilistica precedente come segue:
che si legge così:
“la probabilità che il soggetto sia cattolico, sapendo che lo stesso ‘va in chiesa’ di frequente”.
A tale inferenza attribuiamo un grado di probabilità maggiore proprio sulla base della conoscenza della informazione ulteriore a nostra disposizione, costituita dal fatto della frequenza assidua della parrocchia di quartiere.
Per questo motivo tale stima di probabilità è detta probabilità condizionale, perchè è condizionata appunto dalla conoscenza di specifiche informazioni.
Probabilità condizionali “inverosimili”
Dalle informazioni precedenti a nostra disposizione riguardanti il soggetto che abbiamo di fronte, potremmo anche arrivare a concludere che si tratti in realtà del Pontefice!
L’insieme di informazioni a nostra disposizione (individuo maschio, cattolico praticante) di fatto non contrastano con la nostra inferenza (per certi versi, neanche il fatto di venire a sapere che in passato il soggetto abbia avuto dei figli contrasterebbe in forma esiziale con la nostra inferenza, ma lasciamo perdere…).
Se volessimo esprimere in termini simbolici la probabilità di trovarci di fronte al Pontefice, potremmo scrivere:
che si legge:
“la probabilità che il soggetto in questione sia in realtà il Pontefice, sulla base della informazione che è un cattolico praticante”…
Che grado di probabilità potremmo assegnare a tale inferenza?
Sulla base del nostro bagaglio di conoscenze pregresse (che vanno a supportare il nostro “senso comune”) assegneremo un grado di probabilità molto basso, prossimo allo zero, perchè sappiamo che malgrado i cattolici praticanti siano molti, nei fatti solo uno di questi diventa in realtà Papa…
Prendendo per buona la stima fornita da Wikipedia sul numero di cattolici praticanti nel mondo, pari a 1,285 miliardi, la probabilità di trovarci di fronte al Pontefice è quindi pari a:
evidentemente molto bassa, come era lecito attendersi.
Per non confondere “mele con patate” probabilistiche
Ma qui comincia il bello (si fa per dire) e le probabilità condizionali mostrano tutte le loro insidie controintuitive.
Se volessimo calcolare la probabilità condizionale inversa alla precedente, vale a dire la probabilità che il soggetto sia cattolico, sapendo che si tratta realmente del Pontefice (magari in incognito e sotto mentite spoglie), le nostre conclusioni sarebbero diametralmente opposte!
Si tratterebbe infatti di stimare il grado di probabilità della seguente inferenza:
che si legge:
“la probabilità che il soggetto sia cattolico, supponendo che si tratti in realtà del Pontefice”.
Senza necessità di ulteriori calcoli, è semplice dedurre che tale probabilità è praticamente pari a 1, ovvero pari alla certezza:
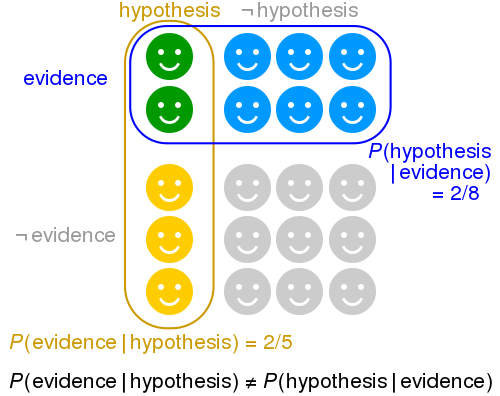
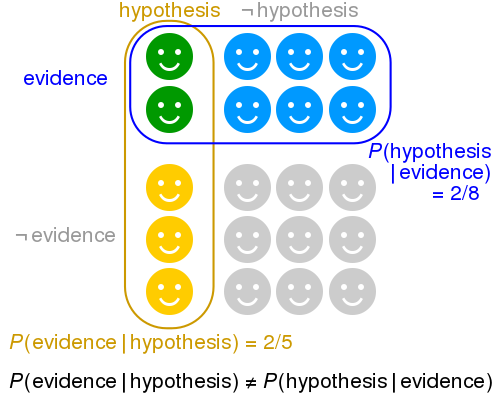
Il problema che spesso si pone quando si ragiona intuitivamente di probabilità condizionali è che si confondono le due diverse probabilità, quella diretta con quella inversa, considerandole erroneamente come interscambiabili (quando invece, come abbiamo appena visto, le due probabilità possono assumere valori addirittura opposti!)
(Image credits: Wikipedia.org)
Pertanto, occorre sempre ricordare che le due probabilità condizionali sono differenti:
È sulla base di questa confusione che spesso vengono tratte conclusioni errate, come appunto l’asserito nesso di casualità tra consumo di cannabis e uso di droghe “pesanti”; anche in questo caso, si confondono tra loro le due diverse probabilità condizionali:
confondendo quindi la probabilità di fare uso di droghe pesanti sulla base di consumo di cannabis, con la probabilità inversa di consumo di cannabis assumendo già abitualmente droghe pesanti!
Per fortuna, non tutti coloro che fanno uso di cannabis finiscono con l’iniettarsi eroina (ma solo una piccola percentuale), così come non tutti quelli che “affettano il filetto finiscono per affettare il cognato…”
Diversamente argomentando, dovremmo vietare il consumo di vino per prevenire l’alcolismo, o meglio ancora, vietare il consumo di cibo per prevenire diabete e obesità…
© Alessandro Parisi - All rights reserved
Vietato l'uso dei contenuti per l'addestramento di Intelligenze Artificiali Generative